匈牙利匹配算法

最大二分匹配

解决问题

找到连接二部图中最多的边数。通常与订单匹配，共享出行的人车匹配相关

算法思想

先找到一条增广路，然后在增广路的基础上取反，即可以多得到一条边。

增广路的前置概念是交替路，什么是交替路呢？顾名思义是交替出现匹配与未匹配的路径。增广路的要求更严格一点，需要从未匹配的边开始，然后经过交替路径最后也是未匹配的边。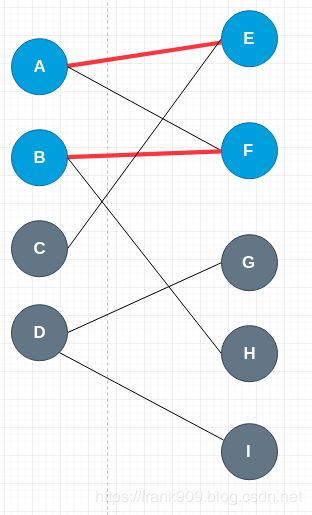

在这张图中，C->E->A->F->B->H 就是一条增广路。

然后增广路取反，也就是匹配与未匹配的边取反，这样就多了一条匹配的路径。

算法代码实现

# G 是临接表的方式表达图形
G={}
G[0] = {0,1}
G[1] = {1,3}
G[2] = {0}
G[3] = {2,4}

match_list = [-1,-1,-1,-1,-1]

label_x = ['A','B','C','D']
label_y = ['E','F','G','H','I']

# v 代表当前的 x 集合中的顶点
# current 代表 y 集合中起冲突的顶点，如果为 -1 则代表没有冲突
def match(v, current):
    for i in G[v]:
        # 如果和已经匹配的节点匹配上了，就跳过，找下一个相连接的节点
        if i == current:
            continue
        
        # 如果可以直接匹配，或者是协调一下就可以匹配，那么就匹配成功，并做标记
        if match_list[i] == -1 or match(match_list[i],i):
            match_list[i] = v
            return True
    # 没有更优的匹配结果，找不到更好的匹配
    return False


def hungarian():
    # 访问 X 集合的顶点
    for i in range(G.__len__()):
        # 对集合中的顶点逐个匹配
        match(i,-1)
    
    for i in range(match_list.__len__()):
        if match_list[i] == -1:continue
        print("%s <--match--> %s:" %(label_x[match_list[i]],label_y[i]))
        


if __name__ == "__main__":
    hungarian()